Conditioned Graph Structures [图结构]

文章中主要提出了一个新的，可解释的，基于图形的VQA模型，最近的VQA方法关注于创建新的注意力结构，复杂性不断增加，但未能对场景中物体之间的语义连接建模

作者将scene structure作为先验知识引入，将bbox对象设为图中的节点，基于问题的图边则通过注意力模块来学习，这不仅确定了图像中与问题相关的最相关的物体，而且还确定了最重要的交互作用(例如相对位置、相似性)，而无需对图形的结构进行任何手工描述

作者认为，学习一个图结构不仅为VQA任务提供了强大的预测能力，而且通过检查最重要的图节点和边，还可以对模型的行为进行解释

Graph Convolutional Neural Networks

Graph CNNs(GCNs)是一个相对较新的概念，用CNN来图结构化数据，GCN分为两类：频率GCN利用图形信号处理的概念，在欧几里得域上定义图形傅里叶变换，允许在频谱域内以乘法的形式进行卷积，频率GCN有所有训练样本的图结构相同的要求；空间GCN更为工程化，需要定义节点排序和patch操作符，文章的目标是学习基于查询上下文的动态图，因此，扩展了edge的概念，使之适应于上下文

Visual Question Answering

Graph-Structured Representations for Visual Question Answering中特别提出了一种基于图的方法，将问题的图表示和抽象图像与图神经网络相结合，并达到了SOTA，这种方法展现了图结构在VQA任务中的潜力，然而，这种方法不容易推广到场景图表示不是先验的自然图像上

BUTD第一次用object proposals作为图像特征，这是VQA Task中的一个重大改进，这样的图像表征已经被利用来通过隐式和显式图结构对对象之间的交互建模，Learning to Count提出了一种基于对象相似性的迭代方法来提高模型的计数能力和可解释性，另一篇Count相关的文章通过proposed features和attention的外积来计算图结构，这两篇文章其实都在做消除重复对象的工作

Methods

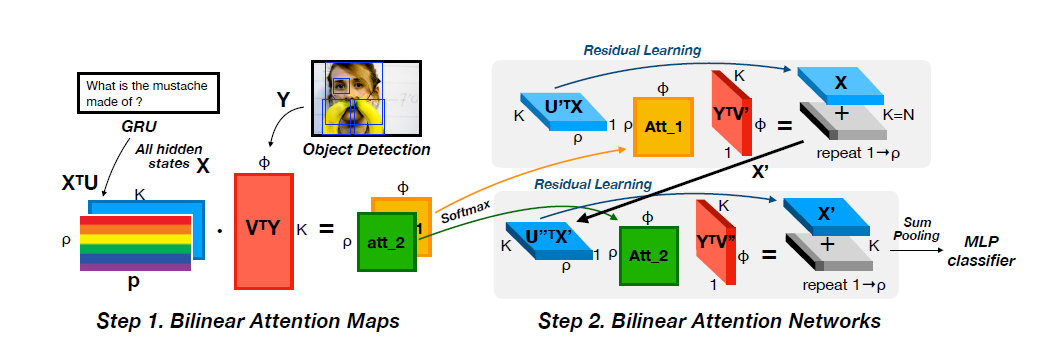
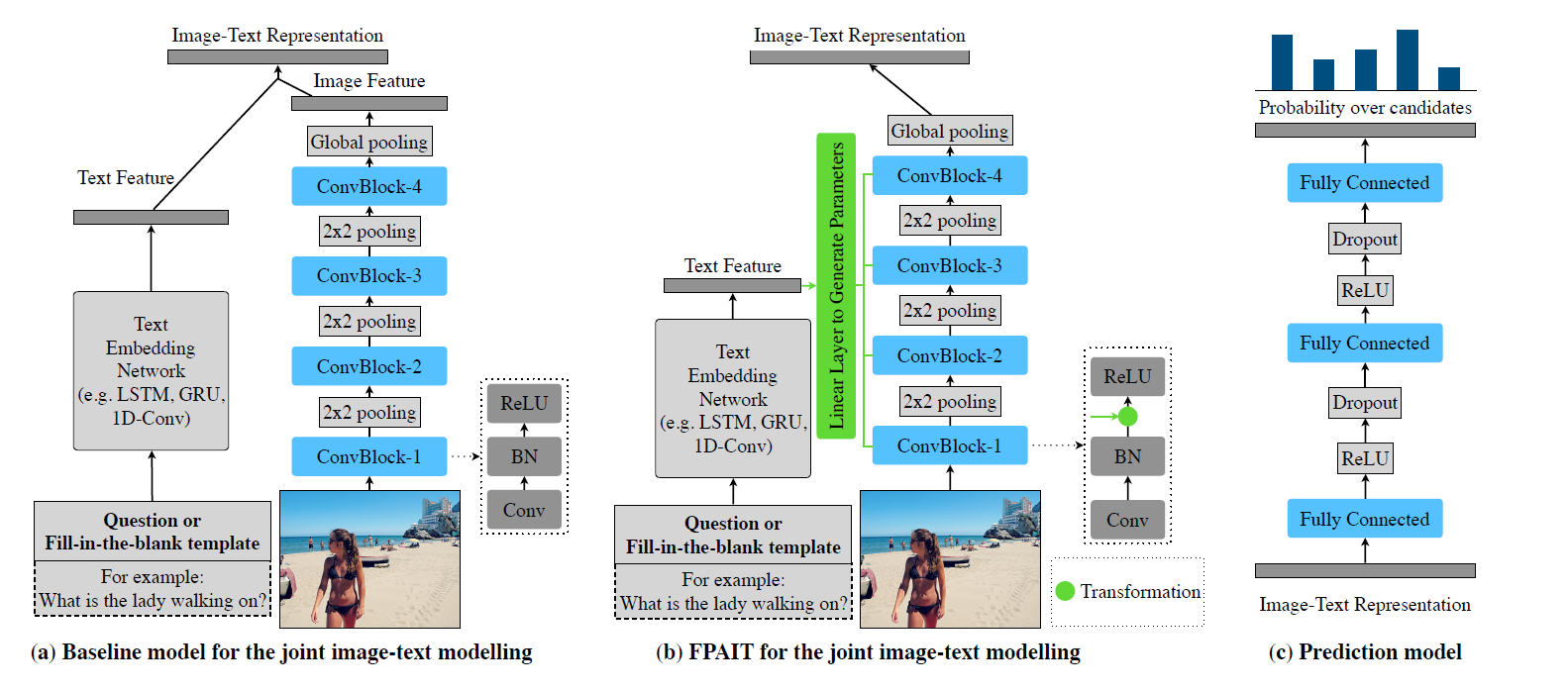
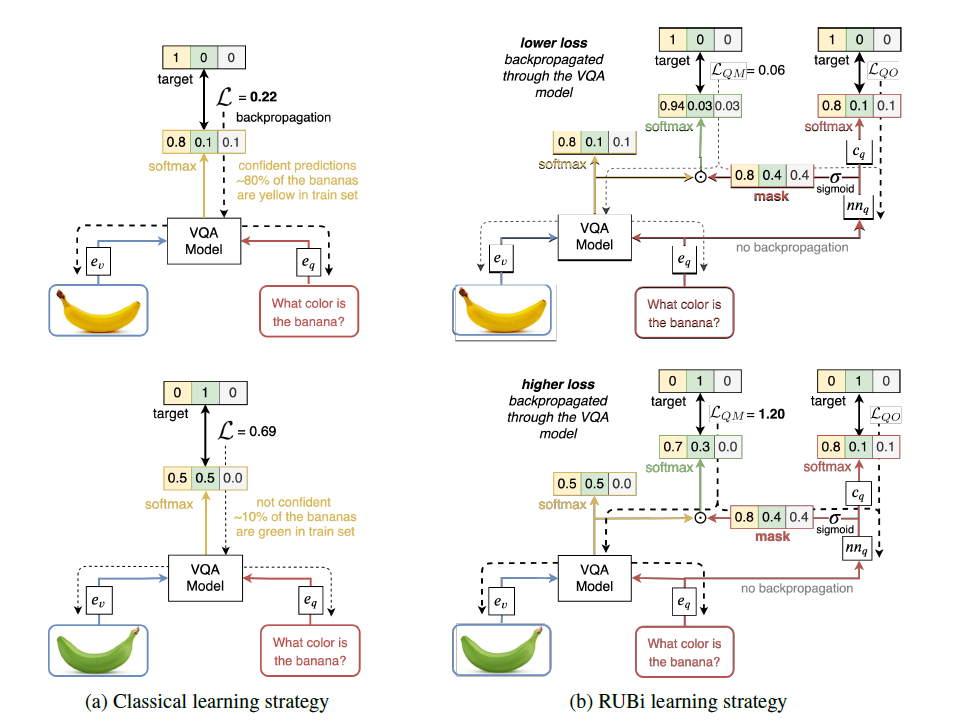
整体框架如图所示

作者提出了一个深度神经网络，它以一种新颖的方式结合了空间、图像和文本特征

首先用word embeddings和RNN来得到问题特征，目标检测得到bbox和图片特征向量，然后图学习模块会学习一个问题相关的图像目标的邻接矩阵，这使得图卷积不仅能关注到对讲，同时能关注到与问题最相关的对象关系，最后，对图卷积特征进行最大池化，和question embedding做元素级乘法来预测答案

Computing model inputs

模型的第一个阶段是计算问题和图片的embedding，先将图片转化为大小为k的视觉特征集，目标检测在模型中是特别重要的步骤，因为bbox构成了图中的点，每个bbox的embedding为卷积特征图的平均值，对于每个问题，用预训练的词嵌入将问题转化为可变长度的嵌入序列，然后用GRU将嵌入序列转化为q的embedding

Graph learner

图学习模块基于问题为图像生成一个图结构，图结构通过定义节点邻域来驱动空间图卷积，这种结构可以自然地学习到一元和成对的注意力，因为邻接矩阵包含自我循环

定义图结构$g={V,\varepsilon,A}$，$\varepsilon$是需要学习的图边，$A \in R^{N \times N}$是邻接矩阵，$v \in V$为每个检测到的图像对象(bbox和特征向量)，模型的目标是学习邻接矩阵$A$，使得每条边都是基于问题的，需要对特征向量之间的相似性以及它们与给定问题的相关性进行建模

首先将embedding q嵌入到N个视觉特征中，记其为$[v_n][q]$，然后计算他们的联合嵌入

$F$是一个非线性函数

然后将所有的embedding拼接在一起得到矩阵$E$，计算邻接矩阵$A=EE^T$

这样的定义对图的稀疏性不施加任何约束，因此可以产生一个全连通的邻接矩阵，接下来需要学习一个图像最相关位置的稀疏图结构

为了学习每个节点的稀疏领域，采取的排序策略为

topm返回的是输入向量的m个最大值的索引，也就是i节点领域中连接最强的节点

Spatial graph convolutions

现在有了一个基于问题的图结构，然后用图卷积的方式来学习新的对象表示，图结构中的顶点v(bbox+特征)最大的特征是在图像中的位置，所以建模他们之间的关系本质上是空间的，同时，许多VQA问题要求模型能够意识到图像中特征的方向和相对位置，这是之前许多方法忽略的问题

因此，作者采用了空间图卷积，直接在graph域中操作，高度依赖于空间关系，用伪坐标函数$u(i,j)$定义对于每个顶点$i$，一个以$i$为中心的坐标系，$u(i,j)$为该系统中顶点$j$的坐标，在系统中$u(i,j)$返回一个极坐标向量$(\rho,\theta)$，表示顶点$i$和$j$相关联的边界框的中心的相对空间位置

作者同时考虑了笛卡尔坐标和极坐标作为高斯核的输入，并观察到极坐标的效果明显更好，作者认为极坐标的不同角度和距离提供了两个解耦的因素来表示空间关系

GCN的关键步骤是定义一个描述每个相邻节点影响的patch算子，该算子对不规则的邻域结构具有鲁棒性，Monti et al提出使用一组可学习均值和协方差的K个高斯核来实现，其中均值在伪坐标下可解释为方向和距离，作者得到每个k的核权值$w_k(u)$，节点i在核k处的patch算子被定义为