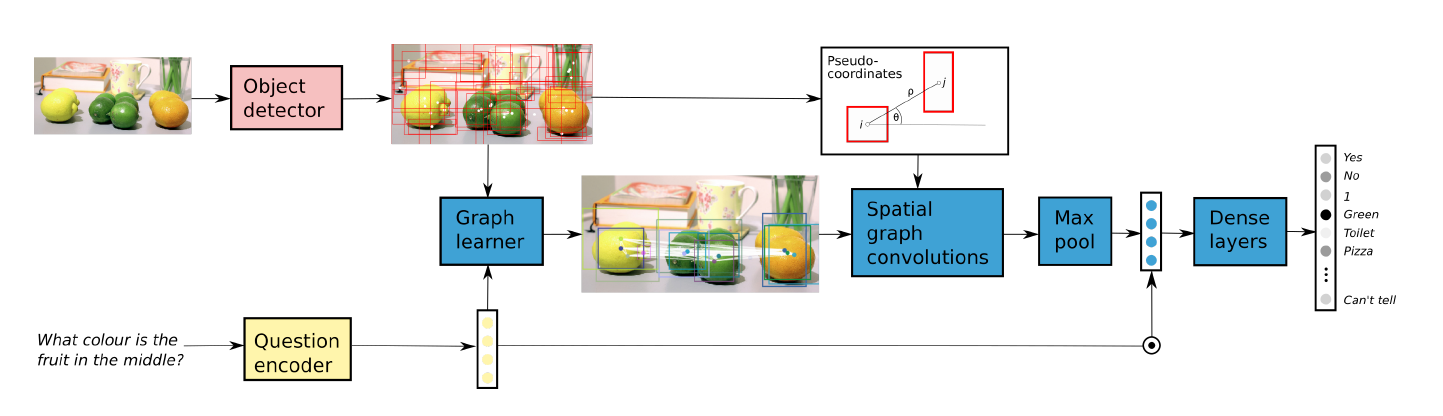
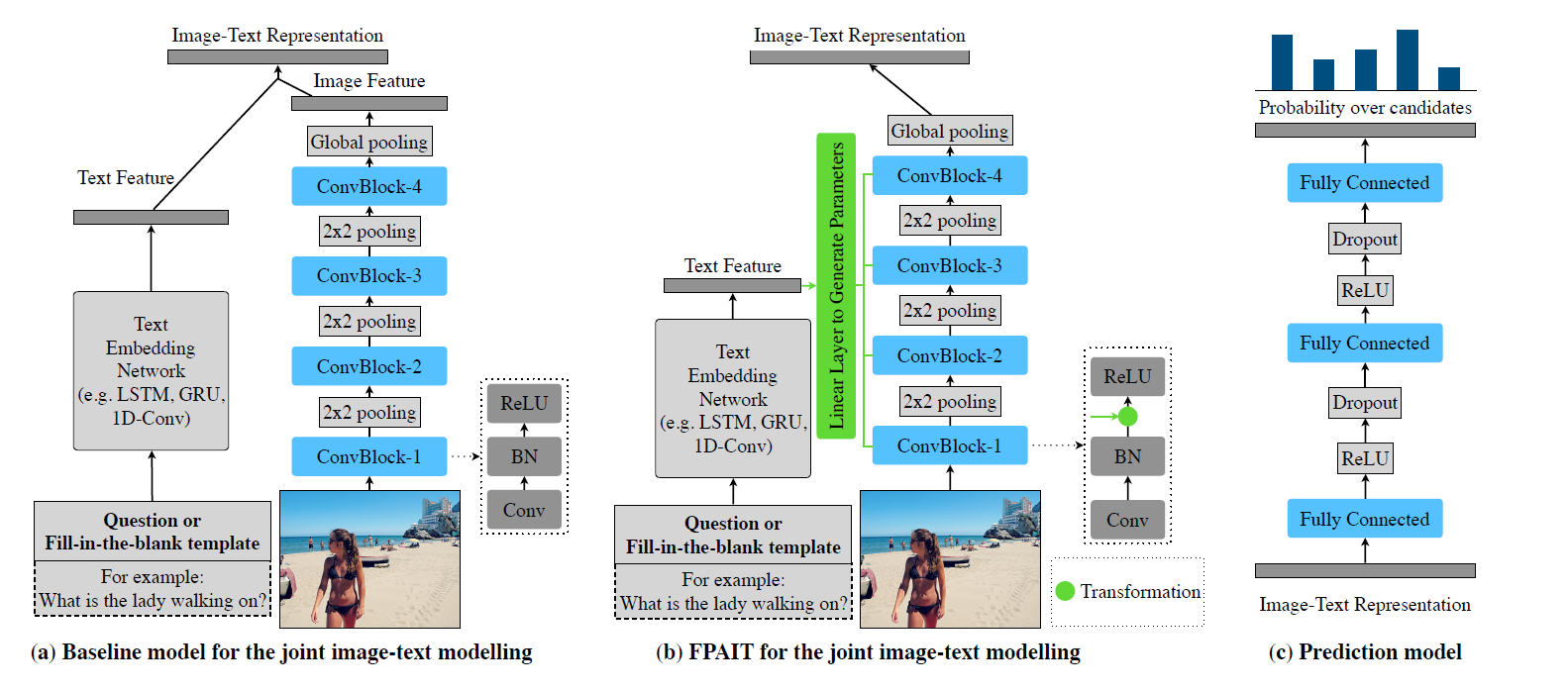
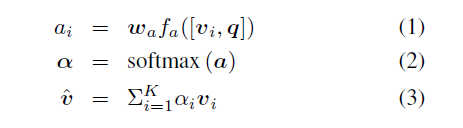BAN [双线性注意力机制]
VQA任务涉及到许多视觉-语言交叉的问题,因此attention在VQA中能够起到比较好的效果,co-attention可以同时推断视觉注意力和语言注意力,但同时忽略了语言和视觉区域之间的交互作用
作者将co-attention扩展为关注问题和图像的每一对多通道的bilinear attention(双线性注意力),如果给定的问题涉及到由多个单词表示的多个视觉概念,则使用每个单词的视觉注意力分布进行推理比使用单个压缩的注意力分布进行推理更能挖掘出相关信息
作者在低秩双线性池化的基础上提出了双线性注意网络,BAN利用了两组输入通道之间的双线性交互,而低秩双线性池提取了每对通道的联合表示,此外作者还提出了一个多模态残差网络MRN来更有效地利用多重双线性注意图
BAN中用residual summations替代了concatenation,以更高效的参数和性能学习了eight-glimpse BAN,图中展示了一个two-glimpse BAN

文章主要贡献如下:
在低秩双线性池化技术的基础上,提出了学习和利用双线性注意分布的双线性注意网络
提出了一种多模态残差网络(MRN)的变种,以有效地利用由模型产生的多双线性注意图,并成功地利用了多达8个注意力地图
在VQA2.0上实现了SOTA,评估了双线性注意图在Flickr30k Entities上性能,推理速度提高了25.37%
Low-rank bilinear pooling
低秩双线性池化算法使用单通道输入(question vector)组合其他多通道输入(image features)作为单通道中间表示(attended feature)
Low-rank bilinear model
先前有研究提出了一个低秩双线性模型来降低双线性权矩阵$W_i$的秩,从而给出正则性,$W_i$被替换为两个更小矩阵的乘法$U_iV_i^T$,这里$U_i \in R^{N \times d}$,$V_i \in R^{M \times d}$, 这种替换使得$W_i$的秩$d \le min(M,N)$,标量输出$f_i$为

式子中的$1$是一个只包含1的向量,$\circ$ 表示Hadamard积 (element-wise multiplication)
Low-rank bilinear pooling
对于向量输出f,引入了池化矩阵P

$P \in R^{d \times c}$,$U \in R^{N \times d}$,$V \in R^{M \times d}$
通过引入$P$作为向量输出$f \in R^c$允许U和V是二维张量,显著减少了参数的数量
Unitary attention networks
注意力机制通过有选择地利用给定的信息来减少输入通道,假设有一个多通道输入Y,包含$|{y_i}|$个行向量,用注意力权重$\alpha$从Y中得到单通道$\hat{y}=\sum_i\alpha_iy_i$,注意力权重$\alpha$通过softmax计算得到

$\alpha \in R^{G \times\phi}$,$P \in R^{d\times G}$,$U \in R^{N \times d}$,$x \in R^N$,$1 \in R^{\phi}$,$V \in R^{M \times d}$,$Y \in R^{M \times \phi}$,当$G>1$的时候表示采用了多glimpses(attention heads),那么就有$\hat{y}=||_{g=1}^G\sum_i\alpha_{g,iYi}$,然后$x$和$\hat{y}$用低秩双线性池化来实现联合表示,最后进行分类
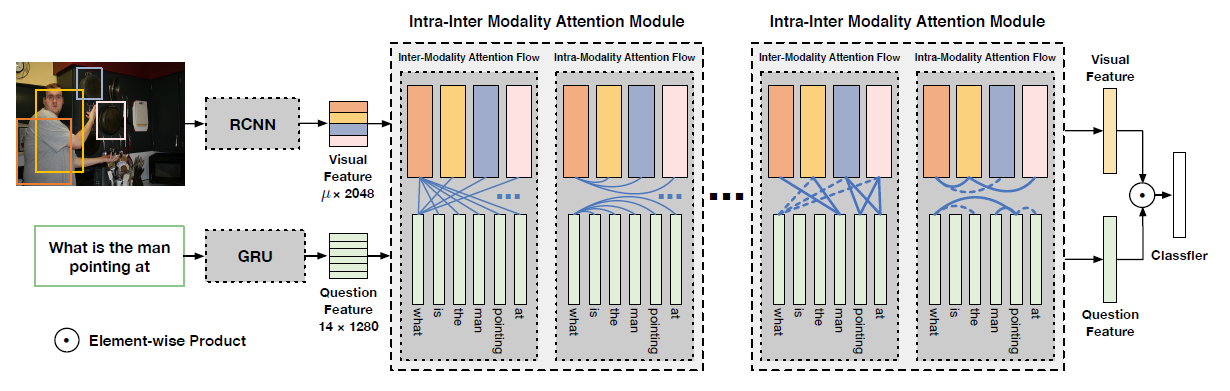
Bilinear attention networks
作者推广了两个多通道输入的双线性模型,$X \in R^{N \times \rho}$以及$Y \in R^{M \times \phi}$,其中$\rho = |{x_i}|$以及$\phi =|{y_j}|$
为了同时减少两个输入通道,作者引入双线性注意映射

其中$U’ \in R^{N \times K}$,$V’ \in R^{M \times K}$,$(X^TU’)_k \in R^{\rho}$,$(Y^TV’)_k \in R^{\phi}$,$f_k’$表示第k个元素的中间表示,矩阵的下标k表示列的索引,$f_k’$也可以写作

然后双线性联合表示$f=P^Tf’$,为方便起见,将双线性注意网络定义为由双线性注意映射参数化的两个多通道输入的函数
$BAN(X,Y;A)$
Bilinear attention map
前文提到的注意图为

$softmax$前的每个$A_{ij}$都是通过低秩双线性池化得到的

多双线性注意图可以扩展为

其中$U$和$V$的参数是共享的,但$p_g$不共享,其中$g$表示glimpses的索引
Residual learning of attention
作者使用MRN的变体从多重双线性注意图中得到联合表示,第i+1次的输出可以表示为

$f_0=X$,$1 \in R^\rho$
对最后一次输出的通道维度求和,就能得到分类器的输入
Time complexity
$BAN$的复杂度等于一个多通道的输入大小$O(KM\phi)$
Related works
Multimodal factorized bilinear pooling
Yu et al做低秩双线性池化时移除了投影矩阵$P$,这个操作对$BAN$没有用
Co-attention networks
Xu and Saenko提出了空间记忆网络模型,计算问题中每个token和每个图像patch之间的相关性,与本文不同的是,它是对相关矩阵的每一个行向量的最大值进行softmax
现有的co-attention都是对每个模态使用单独的注意分布,忽略了模态之间的相互作用
Experiments
VQA2.0 Validation Score

在VQA2.0上使用的参数量

调参

two-glimpse BAN两次attention map可视化

Flickr30k Entities

在VQA2.0 Test上和SOTA的比较